Ceci est une traduction des explications données par Robert Plomin dans son livre Blueprint.
Au lieu de se concentrer sur les moyennes, les statistiques des différences individuelles se concentrent sur la variabilité. Dans l’étude TEDS sur les jumeaux, nous avons évalué le poids à l’âge de seize ans de 2 000 paires de jumeaux. Leur poids moyen est de 130 livres, mais leur poids varie de 75 livres à 250 livres, comme le montre la figure ci-dessous. La figure montre ce que l’on appelle la distribution normale, la courbe en forme de cloche, avec la plupart des résultats proches de la moyenne et moins de résultats à mesure que l’on se rapproche des extrêmes inférieurs ou supérieurs. La distribution du poids n’est pas tout à fait normale parce que l’épidémie d’obésité est responsable d’un nombre disproportionné d’individus plus lourds. En d’autres termes, la queue de la distribution est plus longue du côté droit.
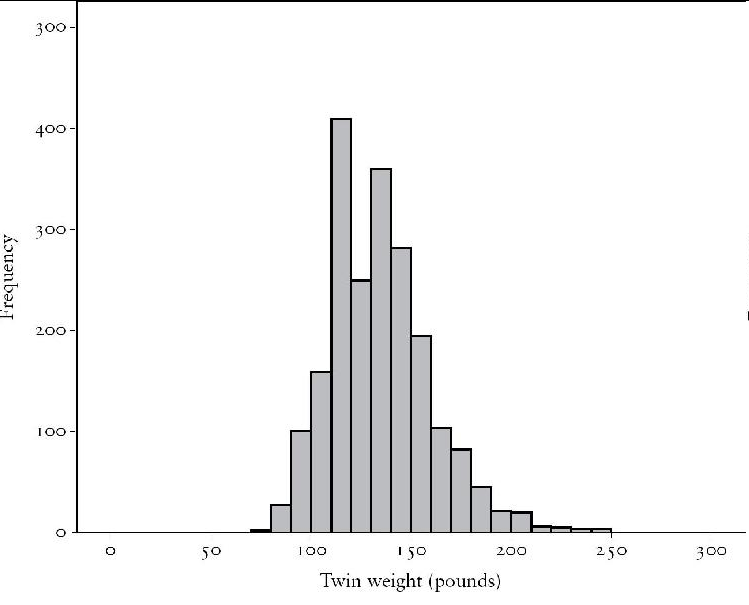
La variance est une statistique qui décrit cette variabilité, c’est-à-dire l’écart entre les poids des individus et leur moyenne. Elle est basée sur la différence de chaque individu par rapport à la moyenne. Un individu qui pèse 130 livres n’ajoute rien à la variance. Une personne qui pèse 200 livres ajoute beaucoup à la variance. Cette personne pèse 70 livres de plus que la moyenne de 130 livres. Cette personne ajoute beaucoup à la variance, car 70 livres au carré, c’est 4 900.
La covariance est essentielle parce qu’elle est un indice de la force de l’association entre deux variables. Elle est appelée covariance parce qu’elle indique dans quelle mesure la variance covarie entre deux variables. Comme nous venons de le voir, la variance est calculée en élevant au carré l’écart de chaque individu par rapport à la moyenne. Pour calculer la covariance, l’écart de chaque individu par rapport à la moyenne sur une variable est multiplié par l’écart de l’individu par rapport à la moyenne sur l’autre variable. La covariance est la moyenne de ces produits pour tous les individus. Ainsi, la covariance sera importante si les personnes qui sont bien au-dessus de la moyenne sur une variable sont également bien au-dessus de la moyenne sur l’autre variable.
La corrélation est la proportion de la variance qui est covariante. Elle divise la covariance par la variance, ce qui convertit proprement la covariance pour la rendre plus facile à interpréter sur une échelle de zéro à un. Si les deux variables covarient complètement, la covariance est égale à la variance et la corrélation est de 1. Vous pouvez visualiser une corrélation à l’aide d’un diagramme de dispersion. Vous avez certainement remarqué que les personnes de grande taille sont plus lourdes. La figure suivante montre un diagramme de dispersion entre le poids et la taille des jeunes de 16 ans de mon étude de jumeaux TEDS.
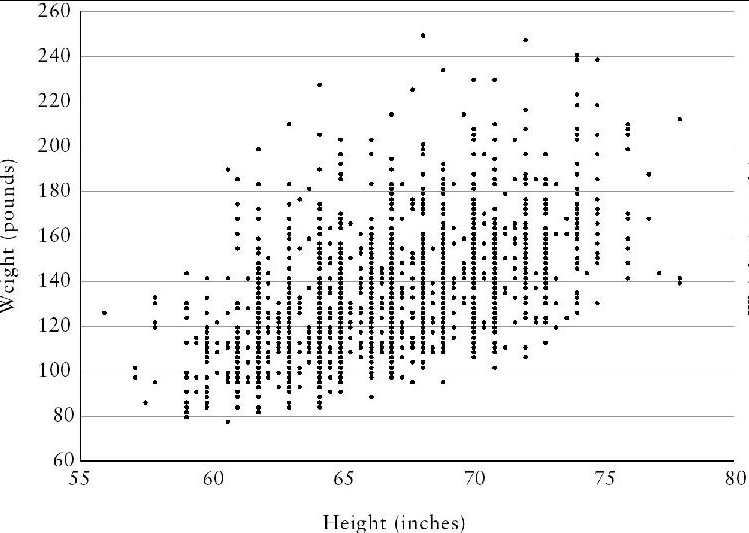
La corrélation est de 0,6, ce qui signifie que 60 % de la variance du poids et de la taille covarient. Si la corrélation était de 0, le nuage de points serait rond plutôt qu’ovale, ce qui indiquerait qu’il n’y a pas d’association entre les deux variables. Si la corrélation était de 1, le nuage de points serait simplement une ligne droite. Les scores de poids peuvent parfaitement prédire la taille, et vice versa.
La corrélation de 0,6 se situe entre ces deux extrêmes. La figure montre clairement que les personnes plus lourdes sont plus grandes, mais il y a des exceptions. Par exemple, le point en haut au centre est l’un des jeunes de seize ans les plus lourds, pesant 250 livres, qui n’est que de taille moyenne. Le poids étant étroitement lié à la taille, il est souvent ajusté en fonction de la taille afin d’obtenir une mesure plus pure du poids indépendamment de la taille. L’un des ajustements les plus répandus est l’indice de masse corporelle.
