La complexité : comprendre la réalité au travers de l’association des disciplines.

Ilya Prigogine parle dans Les lois du chaos¹ d’une certaine dualité entre sciences naturelles et sciences humaines. Certains parlent d’ailleurs de sciences dures et de sciences molles, de sciences exactes et de sciences inexactes.

Dans les sciences naturelles, l’idéal traditionnel était d’atteindre la certitude associée à une description déterministe. Même la mécanique quantique correspond à cet idéal. En revanche, les notions d’incertitude, de choix, de risque dominent les sciences humaines, que ce soit l’économie ou la sociologie.

_{Les lois du chaos, Ilya Prigogine, 1ère édition 1993, éditions Flammarion 2008, p. 17.}

En effet, nous l’avons vu dans l’article sur la complexité, il y a une opposition farouche entre divers champs scientifiques du fait qu’ils s’estiment chacun meilleur que l’autre, en ceci que leur méthodologie serait plus solide, ou que leur éthique serait plus infaillible, etc. Toute une panoplie d’arguments existent, et ici ne sera pas le lieu de tous les lister. Personnellement, et j’écris cet article afin d’éclaircir les raisons de cette opinion, je considère qu’on ne doit plus opposer les sciences mais au contraire rechercher leur complémentarité, d’autant plus quand ces sciences parlent des mêmes objets. Ce que rapporte Hugues Duffau dans l’erreur de Broca², neurochirurgien, montre bien ce phénomène de cloisonnement des sciences.

A l’inverse, dans les autres congrès de neurosciences où je suis également invité, les intervenants se succèdent allègrement à la tribune pour parler des réseaux des neurones, des bases neuronales du langage ou de la “théorie de l’esprit”, mais aussi bien sûr de la neuro-imagerie et des progrès en ce domaine, comme l’état de repos, la connectomique (cartographie des réseaux), mais pratiquement aucun de ces thèmes n’est mis en relation avec… le traitement des pathologies !

Autrement dit, les communautés de la recherche vivent cloisonnées à l’intérieur des lieux de pouvoir où elles ont émergé. La science transdisciplinaire n’existe que très peu dans les faits.

_{L’erreur de Broca, Hugues Duffau, 2017, p. 214-215.}

Dans l’article sur la complexité, je parle des différents niveaux de compréhension d’un même phénomène, et il n’existe pas une science capable d’étudier chaque niveau sans avoir l’aide d’autres disciplines. Ainsi on ne peut pas penser la propagation d’un virus comme le COVID-19 qu’en termes épidémiologiques. Il faut nécessairement un regard sociologique pour comprendre pourquoi de nombreux individus se rencontrent et donc se le transmettent, il faut un regard économique pour comprendre pourquoi certains font fi du virus et vont travailler même en étant malades, il faut un regard psychologique pour comprendre ce que chacun comprend du virus, il faut une connaissances des réseaux sociaux et médias d’information qui propagent de fausses infos provoquant des augmentations de contaminations, etc.

Juste connaître le profil viral du COVID-19 ne permet pas de comprendre totalement pourquoi il se propage, pourquoi nous n’arrivons pas à nous en débarasser, pourquoi il mute, etc.

Seule une alliance de diverses disciplines, issues des sciences dure et des sciences molles (j’utilise ces termes afin d’être le plus compréhensible possible) permettra de réellement approcher d’une compréhension la plus totale du phénomène. Je vous recommande fortement de lire mon article sur la complexité afin de voir plus en détail à quel point il peut être compliqué d’appréhender même les questions les plus banales en apparence, je continue maintenant sur le cœur de l’article.

Le chaos et ses lois.

Je vais essayer d’expliquer en quelques mots ce qu’est la théorie du chaos. James Gleick, historien des sciences, a déjà fait le travail d’écrire sur cette théorie et en a fait un livre éponyme³. Il y décrit le cheminement ayant mené à elle, les différents scientifiques ayant œuvré ensemble ou non, les étapes clés, etc. Il y écrit que

Là où commence le chaos s’arrête la science classique. Depuis qu’il existe des physiciens étudiant les lois de la nature, le monde a été particulièrement ignorant du désordre de l’atmosphère, de la mer turbulante, des variations des populations animales, des oscillations du cœur et du cerveau. L’aspect irrégulier de la nature, discontinu et désordonné, est resté une énigme ou, pis, a été perçu comme une monstruosité.

_{La théorie du chaos, James Gleick, 1ère édition 1987, éditions Flammarion 2008, p. 18.}

De la même manière que le déterminisme est une notion qui transcende de nombreux domaines, de la physique de Newton à la sociologie de Bourdieu, le chaos englobe de nombreux champs d’études comme ceux énoncés dans la citation de James Gleick. Cette théorie fait partie d’une branche des mathématiques qui étudie les systèmes dynamiques.

La définition la plus pertinente d’un système est peut-être qu’il représente un tout composé de plusieurs parties/membres. Cette définition fait ressortir la distinction entre un système et les systèmes : alors que le premier représente l’ensemble (le système), les seconds composent l’ensemble (composants, systèmes et sous-systèmes). Les composants d’un système dépendent également d’autres composants⁴. Imaginez des poupées russes.

Les systèmes dynamiques (comme le corps humain, une famille ou un pays) évoluent dans le temps. Deux caractéristiques de ces systèmes sont importantes :

• Ils sont déterministes, c’est à dire que les évènements passés et présent influencent directement le résultat de l’évolution du système.
• Peu importe les données de départ, deux systèmes aux causes similaires obtiennent des effets similaires.

Ainsi, si l’on imagine une balançoire pendant qu’un enfant l’utilise, nous n’avons pas de mal à imaginer sa possible trajectoire. Les caractéristiques de départ seront toujours à peu de choses près les mêmes, caractéristiques propres à la balançoire, poids et force de l’enfant, etc. Après des milliers de simulations nous pourront voir des trajectoires toutes très similaires, quasiment identiques. L’évolution de la balançoire est déterministe, et les données de départ importent peu pour comprendre son comportement et le prédire.

Maintenant, imaginons une balançoire où l’on ne serait pas directement assis comme on a l’habitude, mais plutôt relié à elle par plusieurs points, disons deux. Voyons à quoi ressemblerait ce “double pendule humaine”. La position de départ, ainsi que toutes les variables (poids, longueur, etc), des trois pendules est quasiment identique mais pas à 100%.

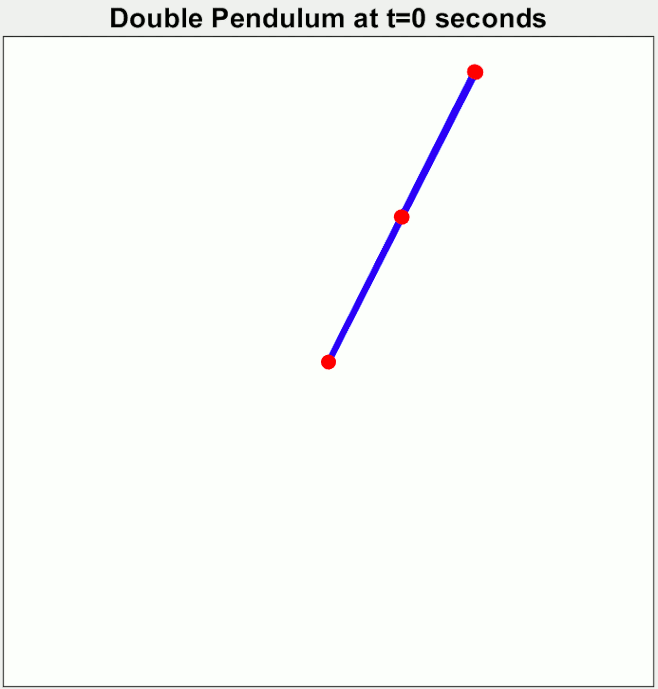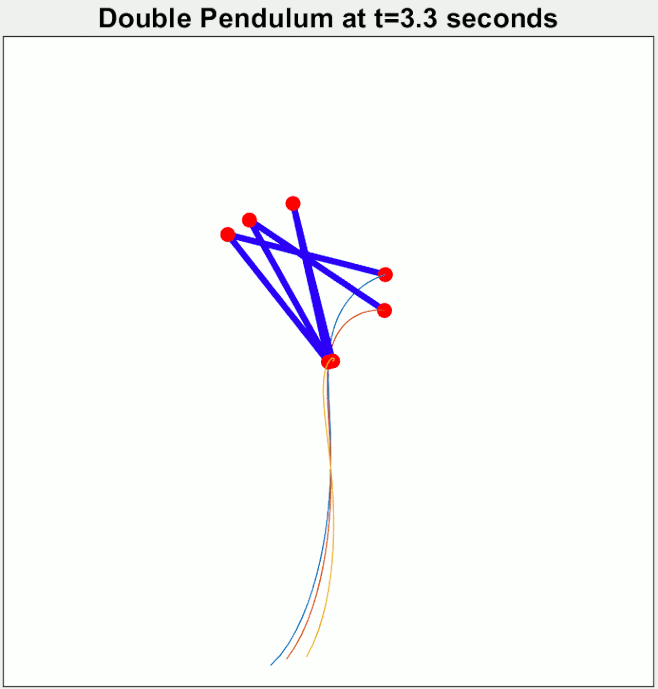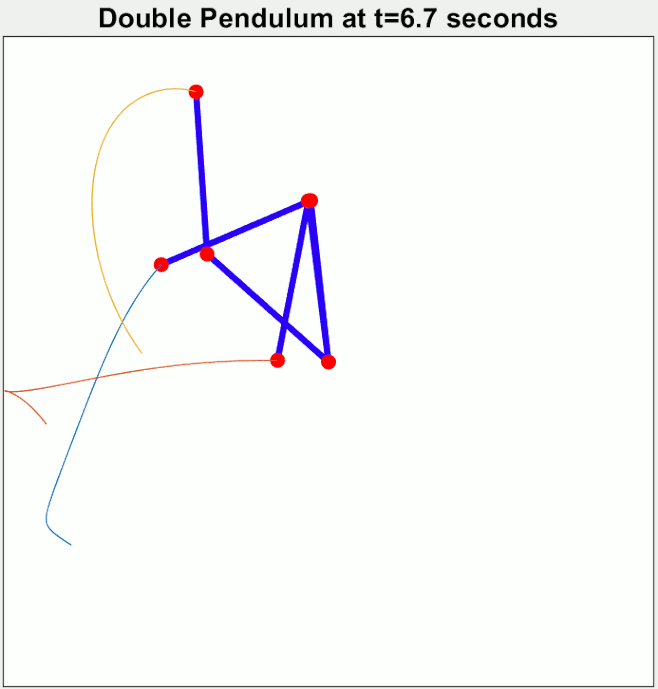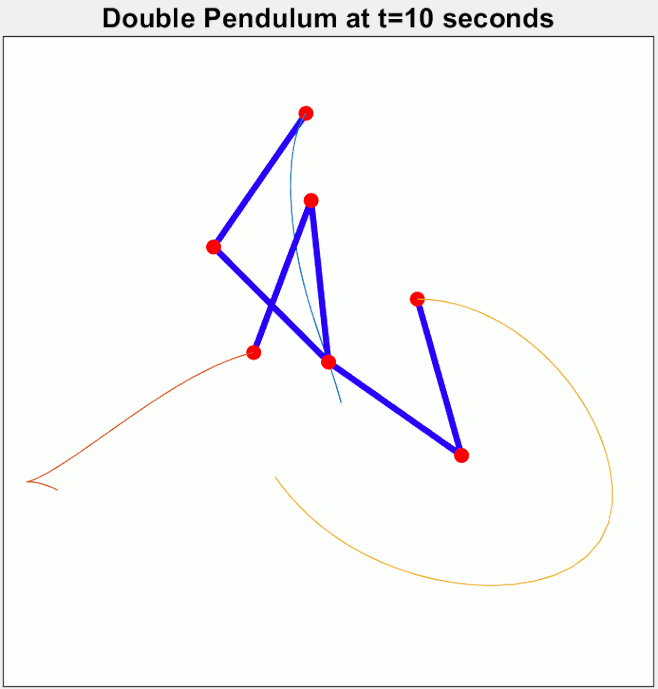
L’exemple ici montre trois comportements très différents (et dont la différence se marque très rapidement).

• Cela semble irrégulier et imprévisible
• Le système est extrêmement sensible aux caractéristiques de départ

C’est un système dit chaotique.

Vous connaissez de nombreux systèmes chaotiques, comme le climat et l’atmosphère. On ne peut prédire la météo plus de quelques jours à l’avance et avec un certain degré de certitude qui n’atteint jamais 100% sauf au moment où l’on est effectivement sous la pluie. “Est-ce qu’un battement d’ailes de papillon au Brésil peut provoquer une tornade au Texas ?” Pas vraiment, mais en quelque sorte oui, puisque c’est l’ensemble des caractéristiques présentes à l’instant T qui donne le phénomène x. Ainsi le battement d’aile n’est pas suffisant, puisqu’il entre en interaction avec le reste. De plus, il est aussi fort probable que le battement ne fasse que ralentir ou accélérer la survenue du phénomène.

Passer en revue chaque aspect de la théorie du chaos serait peu pratique pour vous et moi (je vous renvoie à la bibliographie si vous voulez creuser plus profond), alors je vais résumer sous forme d’une liste. Voici des définitions de concepts reliés à la théorie du chaos (attention à leur usage, quand on change de discipline leur sens peut aussi changer)⁵ :

• Principe de causalité⁶ : Tout effet a un antécédent, une cause proche.
• Déterminisme⁷ : Proposition philosophique selon laquelle tout événement est physiquement déterminé par une chaîne ininterrompue d’événements antérieurs.
• Espace de phase⁸ : Espace abstrait dans lequel sont représentés tous les états possibles d’un système, chaque état possible du système correspondant à un point unique dans l’espace des phases.
• Sensibilité aux conditions initiales⁹ : C’est le cas lorsqu’un changement dans une variable a la conséquence d’un changement exponentiel dans le système.
• Système linéaire : Un système est dit linéaire lorsque le tout est exactement égal à la somme de ses composants.
• Attracteur : Ensemble vers lequel un système dynamique évolue après un temps suffisamment long.
• Feedback : Une réponse à une information, qui soit augmente les effets (rétroaction positive), soit les diminue (rétroaction négative), soit induit un phénomène cyclique.
• Auto-similarité : Cela signifie qu’un objet est composé de sous-unités et de sous-sous-unités sur plusieurs niveaux qui ressemblent (statistiquement) à la structure de l’objet entier. Cependant, dans la vie de tous les jours, il existe nécessairement des limites inférieures et supérieures sur lesquelles ce comportement autosimilaire s’applique.
• Fractal : Est un objet géométrique satisfaisant deux critères : auto-similarité et dimensionnalité fractionnée.
• Dimension fractale¹⁰ : Soit un objet dans un espace à n dimensions, couvert par le plus petit nombre de sphères ouvertes de rayon r. La dimension fractale est log(N)/log(1/r) lorsque r tend vers 0.

Les systèmes complexes adaptatifs.

Comment passe-t-on du simple au complexe ? Les systèmes complexes qui s’adaptent à mesure que le temps passe regroupent plusieurs principes :

• dépendance aux conditions initiales
• non-linéarité
• émergence
• adaptabilité

L’émergence est une notion qui revient souvent quand on parle de chaos et de complexité. James Gleick en parle dans son livre, en nous partageant que

Les premières découvertes firent prendre conscience que chaque changement d’échelle faisait surgir de nouveaux phénomènes et de nouveaux types de comportements. En physique des particules, ce processus ne s’est jamais arrêté : tout nouvel accélérateur, en apportant un accroissement d’énergie et de vitesse, étend le champ de vision de la science à des particules plus petites et sur des échelles de temps plus brèves, et chaque extension paraît fournir une information supplémentaire.

_{La théorie du chaos, James Gleick, 1ère édition 1987, éditions Flammarion 2008, p. 170.}

L’émergence domine notre quotidien. Par exemple, l’association de suffisamment d’individus pour construire et maintenir des mégalopoles. Tous les comportements individuels mis ensemble et organisés d’une manière ou d’une autre donnent un résultat supérieur à la simple addition de tous ces comportements. Les systèmes adaptatifs complexes finissent par se transformer en de nouveaux états une fois qu’ils ont appris à s’adapter à leur nouvel environnement.

Ces systèmes complexes ont la particularité d’être sensibles aux paramètres de départ (qui peuvent s’avérer difficiles à connaître en fonction du ou des systèmes étudiés). Cette sensibilité implique une certaine imprévisibilité dans le comportement du système et conditionne une non-linéarité.

Des changements infimes peuvent avoir de grandes conséquences dans le futur, mais il est important de garder à l’esprit qu’ils peuvent aussi ne pas en avoir, et même que de grands changements puissent avoir de faibles effets. Tous les paramètres n’ont pas la même importance dans l’évolution du système, comme peuvent le montrer Les limites à la croissance¹¹ lorsque l’on parle du climat et de la consommation des ressources terrestres.

Y a-t-il des lois du chaos ? Le chaos n’est-il pas par définition “imprévisible” ? […] mais ce que je voudrais souligner ici, c’est le rôle fondamental du chaos à tous les niveaux de description de la nature, et ce, que ce soit au niveau microscopique, macroscopique ou cosmologique.”

_{Les lois du chaos, Ilya Prigogine, 1ère édition 1993, éditions Flammarion 2008, p. 15.}

De plus, ce qui émerge du système le rend irréductible à ses différentes parties. Un système n’est pas que la simple addition de ses parties, il en est plutôt le produit comme expliqué plus tôt. L’auto-organisation implique qu’aucun élément constitutif du système (ou quoi que ce soit d’extérieur au système) n’a un contrôle direct ou exclusif sur ses modèles collectifs ou sur la façon dont ces modèles évoluent.

Cela signifie également que les interactions entre les constituants du système ne sont pas contrôlées de manière centralisée, mais plutôt locale ; ce caractère local est lié à des dimensions physiques ou cognitives. Les modèles collectifs et ordonnés qui émergent par auto-organisation dans les systèmes adaptatifs complexes sont généralement connus sous le nom de propriétés émergentes, c’est-à-dire des propriétés qui apparaissent ou caractérisent un système à un certain niveau à la suite d’interactions ayant lieu à un niveau inférieur.

Chaos, ordre social et désordre physique ?

Le chaos est souvent associé au désordre. De la même manière que l’anarchisme est souvent considéré comme un mouvement désorganisé, mais c’est faux. Il y a de l’ordre dans l’anarchisme, des règles, des lois, des associations, mais pas de dirigeant, pas de grand architecte de la société anarchiste. Le chaos, c’est pareil, il est extrêmement difficile d’y voir de l’ordre, mais même les systèmes chaotiques obéissent à des lois physiques, qui nous échappent parfois tant leur sensibilité à des paramètres qui nous semblent triviaux est grande. Ne pas voir l’ordre ne veut pas dire qu’il n’est pas là, cela peut même nous pousser à vouloir mettre de l’ordre là où il y en a déjà et donc finalement causer du désordre.

L’un des attributs d’un système chaotique est qu’il est capable de s’auto-organiser. Un système chaotique peut sembler aléatoire de l’extérieur, tout comme un système désordonné, mais la différence réside dans la capacité de ce système à s’organiser pour atteindre un état ordonné. Prenons le climat par exemple, qui est un système chaotique. Nous ne craignons pas qu’il y ait un trou dans l’atmosphère qui apparaisse comme ça, sans raison. Nous ne savons pas prédire la météo à partir de quelques jours avec certitude, pour autant on sait bien qu’il y a des choses a priori impossibles. Le système chaotique qu’est le climat évolue bel et bien dans un cadre de lois physiques duquel il ne peut s’affranchir simplement parce qu’il est chaotique et complexe.

La théorie du chaos est beaucoup utilisée en management des organisations.¹² Notamment en termes de stratégie. En effet, il est pertinent de s’intéresser à l’imprévisibilité du chaos quand on décide de travailler dans une organisation où choisir ses investissements est primordial. Comment réduire notre incertitude concernant le futur ? Quelles techniques et stratégies pour y voir plus clair et ne pas être surpris lorsque le cours de l’action s’effondrera ?

Philip Tetlock et Dan Gardner ont travaillé sur cette question de prédiction. Ils ont même écrit un livre sur le sujet, Superforcasting : the Art and Science of Prediction¹³. L’ouverture de leur livre se fait, sans surprise, en grande partie sur la théorie du chaos et son importance dans le raisonnement qui va être déroulé tout au long du livre.

Il voulait dire que si ce papillon particulier n’avait pas battu des ailes à ce moment-là, l’insondable réseau complexe d’actions et de réactions atmosphériques se serait comporté différemment, et la tornade ne se serait peut-être jamais formée – tout comme le printemps arabe n’aurait peut-être jamais eu lieu, du moins pas au moment et de la manière dont il s’est produit, si la police avait simplement laissé Mohamed Bouazizi vendre ses fruits et légumes ce matin de 2010.

Edward Lorenz a fait évoluer l’opinion scientifique vers l’idée qu’il existe des limites strictes à la prévisibilité, une question profondément philosophique. Pendant des siècles, les scientifiques ont supposé que l’accroissement des connaissances devait conduire à une plus grande prévisibilité, car la réalité était comme une horloge – une horloge incroyablement grande et compliquée, mais une horloge quand même – et plus les scientifiques en apprenaient sur ses entrailles, sur la façon dont les engrenages s’engrènent, sur le fonctionnement des poids et des ressorts, mieux ils pouvaient saisir ses opérations avec des équations déterministes et prédire ce qu’elle ferait.

_{Superforcasting : the Art and Science of Prediction, Philip E. Tetlock et Dan Gardner, 2015, p. 9.}

Il est intéressant de voir qu’ils insistent sur le fait que prédictibilité et imprédictibilité ne s’excluent pas nécessairement. Une fois de plus le climat nous sert d’exemple, puisqu’on peut le prévoir jusqu’à un certain point. C’est une manière de dire qu’il est en grande partie imprédictible sans dire qu’il l’est totalement, puisque nous pouvons tout de même nous y fier dans une certaine mesure à laquelle on se plie inévitablement.

C’est pour cela qu’il est utile de penser en termes de probabilité, comme dans le raisonnement bayésien qui sera le sujet d’un autre article. Penser en termes de probabilité permet de réajuster la méthode de prédiction au fur et à mesure des conséquences observées. L’écart entre notre prédiction et le résultat réellement survenu nous donne une idée de notre précision, de notre régularité dans l’approche du 100% de réussite, etc. C’est l’objet du livre de Tetlock et de Gardner que je vous recommande fortement.

Le chaos est-il la réponse à tout ?

Je ne saurai trop insister sur la précaution à prendre quand on cherche à transposer des notions d’une discipline à l’autre. Les analogies sont vite faites et peuvent mener à l’erreur de raisonnement si l’on se hâte sans réfléchir. Pour autant, il serait dommage de ne pas se servir de certaines images mentales qui peuvent nous aider à démarrer une compréhension dans certains domaines parfois trop abstraits au premier abord. Le but de cet article n’est pas de faire croire qu’une famille fonctionne de la même manière qu’un pays ou que l’Humanité tout entière. Le but est de savoir repérer des pattern dont on peut se servir pour justement nuancer ses propos et affiner le regard sur de nombreuses questions à étudier et qui ont tendance à se fondre les unes dans les autres.

L’étude du chaos a un intérêt certain dans les sciences sociales, notamment en psychologie¹⁴, en management des organisations¹⁵, en économie¹⁶, etc. La conclusion d’un papier concernant les sciences politiques résume bien tout l’intérêt, et les limites, de l’application de la théorie du chaos en dehors des mathématiques :

Tout d’abord, cette théorie a été principalement appliquée comme une métaphore pour la description et l’analyse. La rhétorique et la sémantique du chaos ont apporté avec elle un tas de nouveaux concepts et termes particulièrement utiles pour la compréhension des phénomènes politiques, comme les points de bifurcation, la sensibilité aux conditions initiales, l’auto-similarité, les oscillations, les structures dissipatives ou encore l’entropie. Ce nouveau vocabulaire permet au chercheur de développer ses connaissances et d’explorer de nouveaux aspects du phénomène social et politique observé.

En outre, et principalement appliquée dans les domaines des politiques publiques et de la sociologie des organisations, elle introduit une approche plus quantitative. La théorie du chaos fournit de nouveaux outils et méthodes pour le chercheur qui, sur la base de données longitudinales, entend analyser graphiquement l’évolution de systèmes politiques dynamiques. Ces outils graphiques sont très diversifiés, allant des attracteurs de l’espace des phases aux fractales et à l’analyse spectrale et peuvent fournir des compléments utiles aux outils scientifiques plus traditionnels. Plus globalement, les aspects innovants de la perspective chaotique montrent un potentiel scientifique prometteur pour analyser et décrire l’évolution dans le temps des politiques publiques et des institutions politiques, des acteurs et des processus tels que les cycles électoraux.

_{Papier présenté au congrès de l’Association Internationale de Sciences Politiques en 2006 à Fukuoka au Japon.}¹⁷

Conclusion.

Pour conclure, la théorie du chaos, la théorie de la complexité ainsi que la théorie des systèmes dynamiques, bien qu’ayant l’air inaccessibles à ceux qui comme moi ne sont pas des férus de mathématiques ou même de physique, ont un intérêt indéniable dans la compréhension globale du monde qui nous entoure. Et quand j’utilise le terme de monde, je pense aussi au monde social. Il n’est pas nécessaire de savoir lire toutes les équations des physiciens et mathématiciens qui s’identifient parfois comme des “chaoticiens”. Il est surtout nécessaire de comprendre la logique qui sous-tend tout cela, à savoir la non-linéarité qui vient chambouler notre intuition en de nombreuses occasions, le principe d’émergence qui donne des phénomènes comme la démocratie, l’imprévisibilité de systèmes en apparence simple comme le développement de l’enfant, et bien d’autres choses.

Le simple fait de savoir que de tels phénomènes existent et opèrent à différentes échelles, du micro au macro, permet de percevoir de potentiels modèles de la réalité. Je l’ai déjà dit, tous les modèles sont faux, mais certains sont utiles, surtout quand on veut s’attaquer à certains problèmes comme le réchauffement climatique, la raréfaction des ressources, la démographie, les inégalités sociales et économiques, etc. De nombreuses sources partagées ici mentionnent la délicatesse dont il faut faire preuve quand nous voulons utiliser la théorie du chaos dans des disciplines comme la sociologie ou la psychologie, et ces personnes ont raison de mettre en garde.

Pour autant, force est de constater que de nombreux mécanismes chaotiques opèrent à des échelles bien plus petites que l’Univers dans son ensemble, comme dans le cas de la schizophrénie ou encore les marchés boursiers. Que le système observé soit créé par l’humain ou non, nous pouvons remarquer tout ces phénomènes fortement associés au chaos et aux systèmes complexes adaptatifs.

---

[1] : PRIGOGINE Ilya, Les lois du chaos, Flammarion, 2008, 126 pages.

[2] : DUFFAU Hugues, L’erreur de Broca, Pocket, 2016, 240 pages.

[3] : GLEICK James, La théorie du chaos, Flammarion, 2008, 494 pages.

[4] : Caws, P. General systems theory, its past and potential. Syst. Res. Behav. Sci. 2015, 32, 514–521.

[5] : Oestreicher, C. (2022). A history of chaos theory. Dialogues in clinical neuroscience.

[6] : Descartes R. Meditationes de prima philosophia. Cottingham J, Stoothoff R, Murdoch D, trans. The Philosophical Writings Of Descartes. 3 vols. Cambridge, UK: Cambridge University Press; 1988.

[7] : Laplace PS. Essai philosophique sur les probabilités. Truscott FW, Emory FL, trans. A Philosophical Essay on Probabilities. New York, NY: Dover, 1951.

[8] : Poincaré H. Méthode nouvelles de la mécanique céleste. Goroff DL, trans-ed. New Methods of Celestial Mechanics in History of Modern Physics. New York, NY: Springer-Verlag; 1992.

[9] : POINCARE Henri, Science and Method, Thomas Nelson and Sons, 1914, 288 pages.

[10] : MANDELBROT Benoît, Les objets fractals : Forme, hasard et dimension, 1975 1ère édition, 1995, 212 pages.

[11] : MEADOWS Dennis & Donnela, RANDERS Jorgen, Les limites à la croissance (dans un monde fini), éditions Rue de l’échiquier, Paris, 2017, 485 pages.

[12] : Arıcıoğlu, M. A., Erer, B., & Gülnar, N. (2021). A known innovation for strategy: A study on chaos. In Financial Strategies in Competitive Markets (pp. 179-191). Springer, Cham.

[13] : TETLOCK Philip & GARDNER Dan, Superforcasting : The Art & Science of Prediction, Random House Books, 2016, 352 pages.

[14] : Butz, M.R. (1997). Chaos And Complexity: Implications For Psychological Theory And Practice (1st ed.). CRC Press. https://doi.org/10.4324/9781315139012 ;

Robertson, R., & Combs, A. (2014). Chaos theory in psychology and the life sciences. Psychology Press.

[15] : Thietart, R. A., & Forgues, B. (1995). Chaos theory and organization. Organization science, 6(1), 19-31. ;

Banerjee, S., & Erçetin, Ş. Ş. (Eds.). (2012). Chaos, complexity and leadership 2012. Springer Netherlands.

[16] : Faggini, M., & Parziale, A. (2012). The failure of economic theory. Lessons from chaos theory. ;

Klioutchnikov, I., Sigova, M., & Beizerov, N. (2017). Chaos theory in finance. Procedia computer science, 119, 368-375.

[17] : Plaza i Font Joan Pere, Dandoy Régis (2006) Chaos theory and its application in political science, Paper presented at the IPSA World Congress, Fukuoka, Japan (9-13 July 2006).